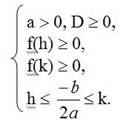Первое занятие!

Назад

При решении квадратных уравнений с параметром необходимо знать следующий теоретический материал.

Для уравнения :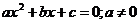
1. Условие существования корней квадратного уравнения, неполные квадратные уравнения.
2. Графическое изображение квадратичной функции и функции, содержащей знак модуля.
3. Расположение корней квадратного трехчлена.
4. Применение теоремы Виета для оценки знаков корней квадратного уравнения.

I. Условие существования корней квадратного уравнения, и графическое изображение квадратного трехчлена.

Неполные квадратные уравнения:

1. c=0; общий вид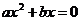
Корни: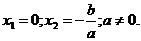

2. c=0, b=0; общий вид: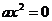
Корни:

3. b=0; общий вид: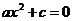
Корни: 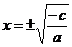при условии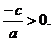

4. a=0, b=0, c=0; общий вид 0x=0; бесконечное множество корней.

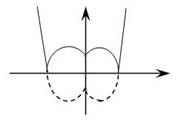
II. Графическое изображение квадратичной функции содержащей знак модуля.

Функция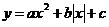
1. Для x ≥ 0 строи график функции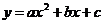
2. Построенную часть графика симметрично отображаем относительно оси 0y (схематичное изображение)

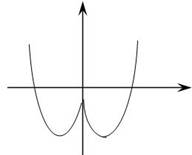
Функция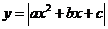
1. Строим график функции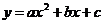
2. Часть графика расположенную ниже оси 0x симметрично отображаем в верхнюю полуплоскость относительно оси 0х(схематичное изображение)

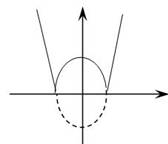
Функция
1. Для x ≥ 0 строим график функции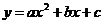
2. построенную часть графика симметрично отображаем относительно оси 0у
3. часть графика, расположенную ниже оси 0х симметрично отображаем в верхнюю полуплоскость относительно оси 0х. (схематичное изображение)

III. Расположение корней квадратного трехчлена. Задачи с ограничениями на корни квадратного трехчлена сводятся к системе рациональных неравенств. При этом для определения необходимых условий, которые накладываются на коэффициенты квадратного трехчлена, исследуются свойства:
- расположение параболы относительно оси 0х;
- значение квадратного трехчлена в некоторых заданных точках (согласно условию);
- положение вершины (оси симметрии) параболы относительно некоторых заданных точек.

1. При каких условиях оба корня квадратного уравнения (необязательно различные) больше некоторого числа h? 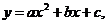, a > 0 (a < 0 рассуждения аналогичны)

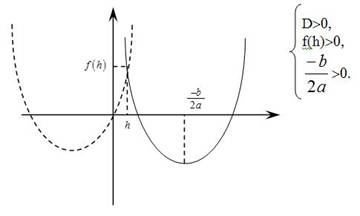
- квадратный трехчлен, график которого изображен пунктиром, удовлетворяет первым двум условиям и не удовлетворяет третьему.
- по данному чертежу можно составить условие существования двух отрицательных корней.

2. При каких условиях оба корня квадратного уравнения , имеющего различные корни не больше некоторого числа h?

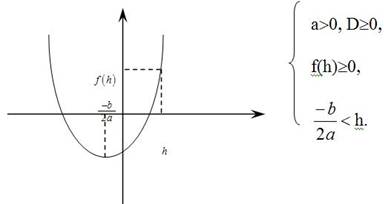
3. При каких условиях корни квадратного уравнения лежат по разные стороны от некоторого числа h?

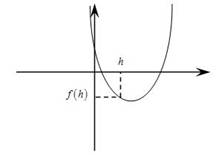
- для того чтобы парабола пересекала ось 0х в двух точках и между ними находилась точка с координатами (h;0) достаточно, чтобы f(h) < 0

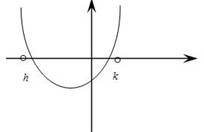
4. При каких условиях оба (можно одинаковых) корня квадратного уравнения принадлежат некоторому отрезку [h,k]?

5. При каких условиях один из двух различных корней квадратного уравнения принадлежит интервалу (h, k)?

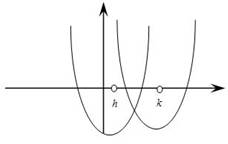
Чтобы один из корней квадратного трехчлена удовлетворял условию задачи, т.е. парабола пересекала интервал в одной точке необходимо, чтобы значения квадратного трехчлена в точках h и k были разных знаков.
Аналогично рассматриваются задачи при условии а < 0 В качестве закрепления отработать каждый случай, когда ветви параболы направлены вниз.

IV. Применение теоремы Виета для оценки знаков корней квадратного уравнения. Теорема: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Приведенное квадратное уравнение: 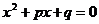. Теорема Виета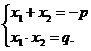
Не приведенное квадратное уравнение: 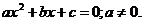. Теорема Виета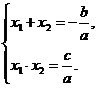
D=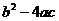 (дискриминант квадратного уравнения).

1. Если квадратное уравнение имеет корни и они положительные, то решаем систему:
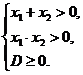(если в условии оговаривается наличие различных корней D > 0)

2. Если квадратное уравнение имеет корни и они отрицательные, то решаем систему:
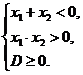(если в условии оговаривается наличие различных корней D > 0)

3. Если квадратное уравнение имеет корни и они разных знаков, то решаем систему:

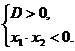
4. Если один из корней квадратного уравнения равен нулю, то решаем систему:

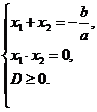
Из второго уравнения находим значение параметра
- Проверка условия, что параметр удовлетворяет D ≥ 0 (при данном параметре корни существуют)
- Полагая, что один из корней равен нулю и найденное значение параметра подставляем в первое уравнение, вычисляем второй корень, делаем вывод о его знаке.

На этом повторение основ теоретического материала можно закончить и отработать полученные знания на конкретных задачах.

Назад