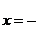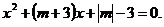Второе занятие!
Цель: Отработать задачи, связанные с условием существования корней квадратного уравнения.
Задание 1.1 Найти все значения параметра а, для которых квадратное уравнение 
1. имеет два различных корня;
2. не имеет корней;
3. имеет два равных корня.
Решение
Так как уравнение квадратное первое условие а≠-2. Наличие корней зависит от дискриминанта, вычислим его значение:
D=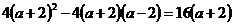 . Исходя из условия существования корней получаем:
. Исходя из условия существования корней получаем:
1. Уравнение имеет два различных корня D > 0, ⇒ 16(a+2) > 0, ⇒ a > -2, что удовлетворяет условию а≠-2.
2. Уравнение не имеет корней, если D < 0, ⇒ 16(a+2) < 0, ⇒ a < -2 что удовлетворяет условию а≠-2
3. Два равных корня, если D=0, ⇒ 16(а+2)=0, ⇒ а=-2, что не удовлетворяет условию (а≠-2). Третий случай места не имеет.
Ответ: два корня, если а∈(-∞-2); нет корней, если а∈(-2;+∞)
Задание 1.2. Найти все значения параметра а, при каждом из которых уравнение
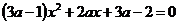 имеет два различных корня.
имеет два различных корня.
Задание 1.3.Найти все значения параметра а, при каждом из которых уравнение
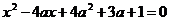 не имеет решений.
не имеет решений.
Задание 1.4.При каких значениях параметра m, только один из корней уравнения равен нулю.
а) 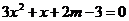
Решение квадратное уравнение имеет один корень равный нулю, если его свободный коэффициент равен нулю, что равносильно 2m-3=0 ⇒ m=1,5.
Уравнение имеет вид: 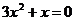
Ответ: m =1,5.
и
Задание 1.4.(для самостоятельного решения)
б)в)
Задание 1.5. При каких действительных значениях параметра m, оба корня уравнения
 равны нулю.
равны нулю.
b=0Уравнение имеет два совпавших корня равные нулю, если коэффициенты
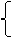 c=0.
c=0.Получаем:
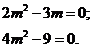 ⇒
⇒ 
 ⇒
⇒ 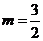
Ответ: m=1,5.
Задание 1.6. При каких действительных значениях параметра m, корни уравнения равны по модулю, но противоположны по знаку (использовать теорему Виета).
а)б)
разделим на 2m не равное 0; получим если корни одинаковы по модулю но привидённое уравнение. Если корни противоволожны по знаку, то по теореме одинаковы по модулю, но противоположны Виета:
. Получаем
по знаку, то по теореме Виета:
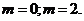
. Получаем
Проверка: 1.
;

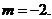
Проверка:
;
2.
;
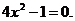
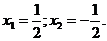
Ответ: m=-2. Ответ: m=0, m=2.