Третье занятие!
ЦЕЛЬ: Отработать приемы графического и аналитического способов решения уравнений с параметром, а также задачи о расположении корней квадратного уравнения, в зависимости от условия задачи.
Задание: Решить относительно уравнение, для каждого значения параметра . В данных уравнениях можно использовать как графический, так и аналитический способ решения.
Задание 2.1. Решить уравнение 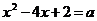
I способ (графический). Основан на том , что правая и левая части уравнения разные по качеству и простые в построении графики функций. Рассмотрим функции 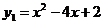 - графиком является парабола, ветви направлены вверх. Для удобства построения выделим полный квадрат
- графиком является парабола, ветви направлены вверх. Для удобства построения выделим полный квадрат 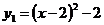 ; вершина параболы точка с координатами
; вершина параболы точка с координатами 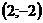 . Рассмотрим функцию
. Рассмотрим функцию 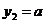 - прямая параллельная 0x. Так как параметр содержится в уравнении прямой, то решение уравнения будет зависеть от расположения данной прямой. Построим графики функций:
- прямая параллельная 0x. Так как параметр содержится в уравнении прямой, то решение уравнения будет зависеть от расположения данной прямой. Построим графики функций:
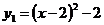 и
и 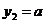 . По графикам построенных функций очевиден ответ.
. По графикам построенных функций очевиден ответ.
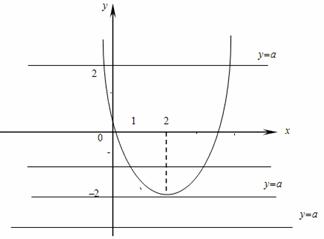
Ответ: 1. нет решений.
2. одно решение.
3. два решения.
При решении графически можно только указать количество корней , но не всегда удается найти их аналитическое значение.
II способ (аналитический). Позволяет определить количество корней и их значение.<
Решить уравнение  . Решение данного уравнения зависит от значения дискриминанта. Найдем его значение:
. Решение данного уравнения зависит от значения дискриминанта. Найдем его значение:
D=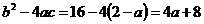 . Получаем
. Получаем
1. D < 0; a < -2 решений нет.
2. D = 0; a = 2 одно решение 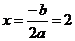 .
.
3. D > 0 a > -2 два решения 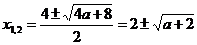 .
.
Задание 2.2. 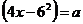 (аналитически и графически). 2.3
(аналитически и графически). 2.3 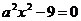 (аналитически и графически).
(аналитически и графически).
Задание 2.3. 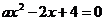 (аналитически)
(аналитически)
Задание 2.4. 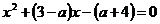 (аналитически)
(аналитически)
Задание 2.5. При каких значениях параметра 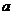 уравнение
уравнение 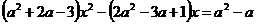 имеет более двух корней?
имеет более двух корней?
Решение: очевидно, что уравнение имеет более двух корней, если оно имеет вид 0х=0. Получаем систему из трех уравнений:
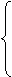
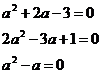 ⇒
⇒ 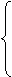
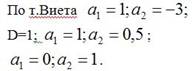 ⇒ a=1.
⇒ a=1.
Ответ: при а = 2 уравнение имеет более двух корней.
Задание 2.6. Найти все значения параметра 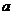 , для которых вершины парабол
, для которых вершины парабол  и
и 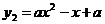 лежат по разные стороны от прямой
лежат по разные стороны от прямой 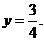 .
Решение: Решение данной задачи начнем с анализа графической модели. Рассмотрим: функция
.
Решение: Решение данной задачи начнем с анализа графической модели. Рассмотрим: функция 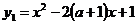 - графиком является парабола, ветви направлены вверх. Функция
- графиком является парабола, ветви направлены вверх. Функция 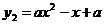 - графиком является парабола, направление ветвей будет зависеть от значения параметра
- графиком является парабола, направление ветвей будет зависеть от значения параметра 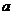 при
при 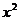 .
.
Согласно условию задачи схематично можно изобразить четыре возможных варианта:
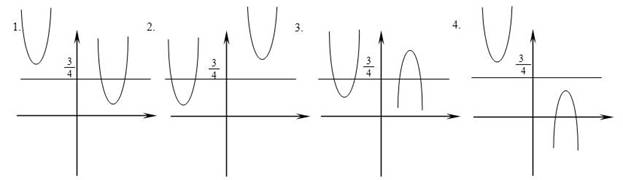
Таким образом можно выделить четыре системы неравенств, где 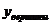 данных парабол лежит выше или ниже оси 0х , с учетом того, что ветви второй параболы могут быть направлены вверх и вниз.
данных парабол лежит выше или ниже оси 0х , с учетом того, что ветви второй параболы могут быть направлены вверх и вниз.
Составим выражение задающее 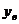 для каждой функции: 1)
для каждой функции: 1) 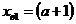 подставим в первую функцию, получаем
подставим в первую функцию, получаем 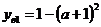 ; 2)
; 2) 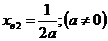 подставим во вторую функцию, получаем
подставим во вторую функцию, получаем 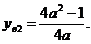
Согласно схематичным чертежам записываем четыре системы неравенств:
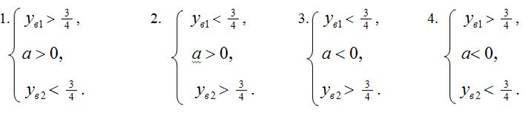
Рассмотрим более подробно решение первой системы . преобразование остальных систем аналогично , отличается только знаками:
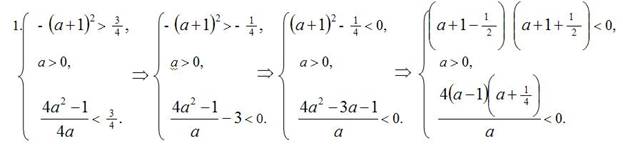
Рационально далее решить систему методом интервалов :
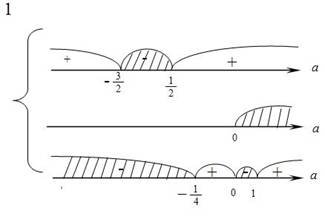
совместных решений нет.
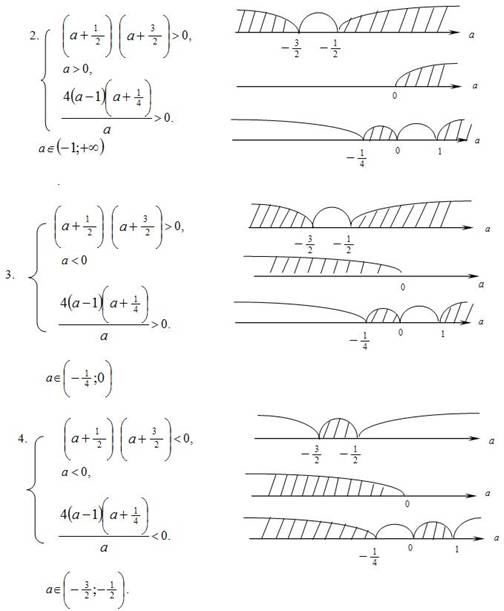
Объединяя решения систем получаем окончательный
Ответ: 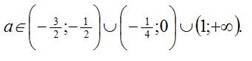
Задание 2.7. Найти все действительные значения параметра а, для которых вершины парабол 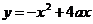 и
и 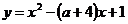 лежат по разные стороны от прямой
лежат по разные стороны от прямой 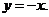 .
.
Решение: Рассмотрим функцию 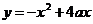 - графиком является парабола, ветви направлены вниз. Найдем точки пересечения с осью 0х:
- графиком является парабола, ветви направлены вниз. Найдем точки пересечения с осью 0х: 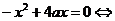
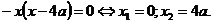 Очевидно, что при x=0 получаем у = 0. Таким образом, график функции
Очевидно, что при x=0 получаем у = 0. Таким образом, график функции 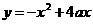 (при любых значениях а) проходит через начало координат. Найдем координаты вершины параболы для того, чтобы оценить ее расположение относительно прямой
(при любых значениях а) проходит через начало координат. Найдем координаты вершины параболы для того, чтобы оценить ее расположение относительно прямой 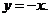 Выделим полный квадрат:
Выделим полный квадрат: 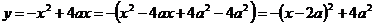 . Координаты вершины
. Координаты вершины 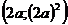 .
.
Замечаем, что ордината вершины есть квадрат абсциссы вершины параболы, следовательно, при любых а≠0, вершина параболы заданной функцией 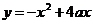
лежит выше прямой 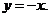
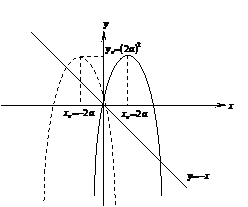
Чтобы выполнялось условие задачи необходимо, чтобы график функции 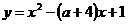 располагался ниже
располагался ниже  То есть имело решение неравенство
То есть имело решение неравенство
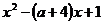 <
<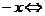
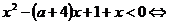
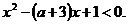 Данное неравенство имеет решение, если ордината вершины параболы заданной функцией
Данное неравенство имеет решение, если ордината вершины параболы заданной функцией 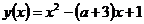 лежит ниже оси 0х. Вычислим интересующую нас ординату:
лежит ниже оси 0х. Вычислим интересующую нас ординату: 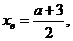 тогда
тогда 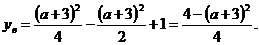 Выполнение условия задачи равносильно неравенству:
Выполнение условия задачи равносильно неравенству: 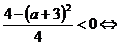
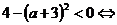
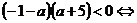

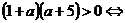 .
.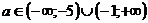 В первой части решения оговаривается условие а≠0, то получаем
В первой части решения оговаривается условие а≠0, то получаем
Ответ: 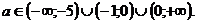
Задание 2.8. Найти все значения параметра а, при которых корни уравнения 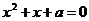 действительные, различные и оба больше а.
действительные, различные и оба больше а.
Решение: Графическая интерпретация данной задачи: Уравнение будет иметь два различных действительных корня, которые одновременно больше а, тогда и только тогда, когда:

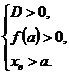 ⇒
⇒ 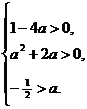 ⇒
⇒ 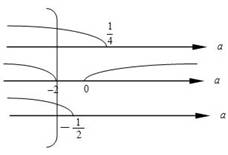
где 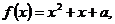 а
а 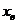 - абсцисса вершины параболы
- абсцисса вершины параболы ![]()
Ответ: 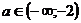 .
.
Задание 2.9. Найти все значения параметра а, при которых корни уравнения 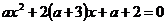 неотрицательны.
неотрицательны.
Решение: Корни уравнения неотрицательны, значит они могут принимать значения больше либо равные нулю, не сказано, что корни различны, следовательно это могут быть два совпавших корня. Графическая интерпретация данной задачи:

Чтобы выполнялось условие задачи, необходимо и достаточно
1) или 2)
или 2) 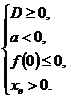 решая системы методом интервалов, получаем:
решая системы методом интервалов, получаем:
1) пустое множество 2) 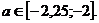
Ответ: 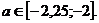
Задание 2.10. Найти все значения параметра а, при которых корни уравнения 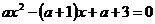 имеют разные знаки.
имеют разные знаки.
Решение: Для того, чтобы парабола, являющаяся графиком функции  , пересекала ось абсцисс в точках, между которыми располагается начало координат, необходимо и достаточно, чтобы квадратный трехчлен
, пересекала ось абсцисс в точках, между которыми располагается начало координат, необходимо и достаточно, чтобы квадратный трехчлен
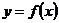 принимал в точке х = 0 отрицательное или положительное значение, в зависимости от направления ветвей параболы. Графическая интерпретация данной задачи:
принимал в точке х = 0 отрицательное или положительное значение, в зависимости от направления ветвей параболы. Графическая интерпретация данной задачи:
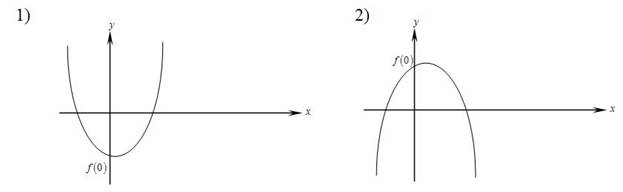
Тогда искомое условие задачи имеет вид:
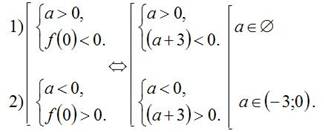
Ответ: 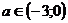 .
.
Задание 2.11. Найти все значения параметра k, при которых уравнение 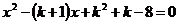 имеет два корня, причем один из них больше 2, а другой меньше 2.
имеет два корня, причем один из них больше 2, а другой меньше 2.
Решение: Предлагаю графическую интерпретацию, составить систему неравенств, удовлетворяющих условию задачи – самостоятельно.
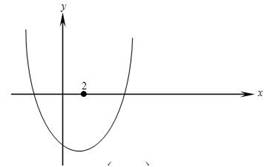
Ответ: 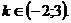
Задание 2.12. При каких значениях параметра а, корни уравнения 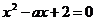 принадлежат отрезку
принадлежат отрезку 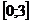 ?
?
Решение: При требуемом условии расположения корней квадратного трехчлена 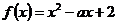 , соответствующая парабола располагается:
, соответствующая парабола располагается:

Решение данной задачи определяется условием: 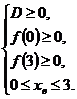 ⇔
⇔ 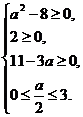 решаем систему методом интервалов, откуда
решаем систему методом интервалов, откуда
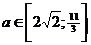
Ответ: 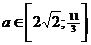 .
.
Задание 2.13. При каких значениях параметра а корни уравнений 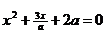 и
и 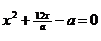 не перемежаются (уравнения имеют по два различных корня; между корнями одного нет корней другого)?
не перемежаются (уравнения имеют по два различных корня; между корнями одного нет корней другого)?
Решение: Положение графиков функций 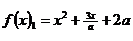 и
и 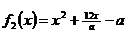 при требуемых ограничениях на корни изображается графически следующим образом:
при требуемых ограничениях на корни изображается графически следующим образом:
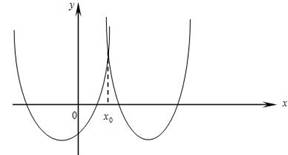
Найдем абсциссу 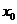 точки пересечения данных графиков:
точки пересечения данных графиков: 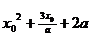 =
=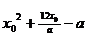 ⇔
⇔ 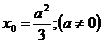 .Тогда расположение пар корней, когда они не перемежаются, определяется условиями:
.Тогда расположение пар корней, когда они не перемежаются, определяется условиями:
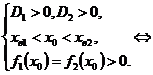
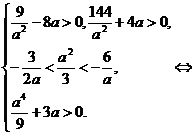
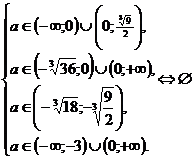
Ответ: а ∈ пустому множеству.
Задание 2.14. Найти все значения параметра а, при каждом из которых все корни уравнений 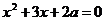 и
и 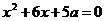 различны и между двумя корнями одного из них находится ровно один корень другого.
различны и между двумя корнями одного из них находится ровно один корень другого.
Решение: Положение графиков функций 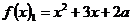 и
и  при требуемых ограничениях на корни изображается графически следующим образом:
при требуемых ограничениях на корни изображается графически следующим образом:
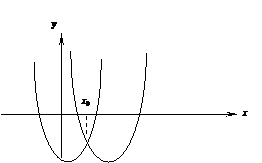
Найдем абсциссу 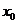 точки пересечения данных графиков:
точки пересечения данных графиков: 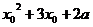 =
=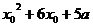 ⇔
⇔ 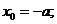 когда они перемежаются, определяется условиями:
когда они перемежаются, определяется условиями:
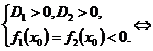
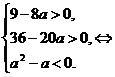
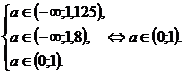
Ответ: а∈(0;1).