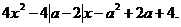Четвёртое занятие!

ЦЕЛЬ: Систематизировать и закрепить правила построения графиков квадратичных функций. Отработать графический способ решения квадратных уравнений с модулем на нахождение количество корней уравнения (если возможно найти аналитическое выражение корней).

С точки зрения практического решения графики, в данных задачах, наиболее наглядно представляют ответ на поставленную задачу, при решении любых уравнений необходимо, по возможности, решение представлять и графически. Это позволяет учащимся наиболее полно увидеть результат своей работы.

Зачастую аналитическое выражение корней лучше понимается после их графического изображения.

Задание 3.1. Найти все значения параметра а, для которых уравнение 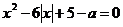имеет хотя бы один корень.
Решение: сразу оговариваем, что “хотя бы один корень” это значит один и более. Данное уравнение рационально решать графически т.к. уравнение можно представить в виде двух функций, графики которых четко выражены и удобны для построения.
Рассмотрим функции 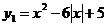и .
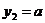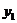- квадратичная функция, правила построения графика рассмотрены ранее, 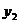- графиком является прямая параллельная оси 0х. Параметр содержится во второй функции, поэтому количество корней (точек пересечения графиков) будет зависеть от расположения прямой
у = а . Строим графики и проводим анализ данных.

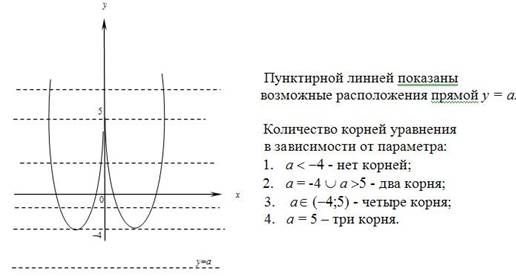
Для самостоятельной работы:
Задание 3.2. Найти все значения параметра а, для которых уравнение 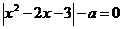имеет ровно три действительных корня.

Задание 3.3. Найти все значения параметра а, для которых уравнение 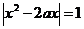имеет три действительных корня.
Решение.В данном случае параметр содержится под знаком модуля, исследовать расположения квадратичной функции в зависимости от параметра объемная работа, поэтому сначала рационально решить аналитически. Уравнение равносильно совокупности уравнений 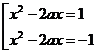. 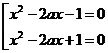; 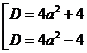проанализируем значение дискриминанта каждого из уравнений.
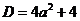>0 для любых значений а т.о. первое уравнение всегда имеет два корня. Чтобы первоначальное уравнение имело три корня во втором уравнении должно быть два совпавших корня, следовательно ; a=
Ответ: при а= уравнение имеет три действительных корня.
Графический способ решения 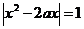. Рассмотри графики функций 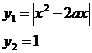, зная схематичное изображение графиков обоих функций имеем вид:

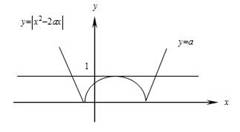
Очевидно , что уравнение имеет три корня если 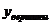параболы лежит на прямой у = 1.
Рассмотрим 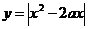выделим полный квадрат , чтобы определить координаты вершины:
.
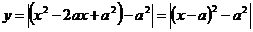Согласно правилам нахождения вершины параболы в нашем случае вершина (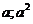), ограничений на значение параметра а нет. Возможны два варианта (с учетом знака абсолютной величины)
а > 0:(1;1) или а < 0: (-1;1) , следовательно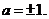

Задание 3.4. a) При каких значениях параметра а уравнение 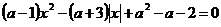имеет три различных действительных корня.
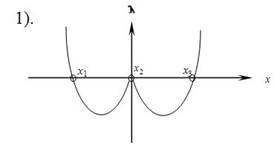
Решение: Начнем с графического изображения. Зная правила построения графика функции 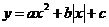и общий вид данного графика , три различных корня могут быть если график имеет вид

Остальные варианты расположения графика не подходят.

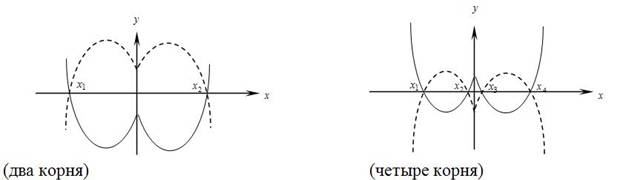
При решении нашего уравнения это возможно если свободный коэффициент

; тогда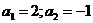

. Рассмотрим два случая:
1). При а = 2: графиком функции

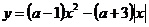при х ≥ 0 является парабола, ветви направлены вверх.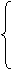

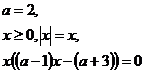из последнего уравнения

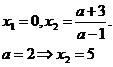в силу симметричности

.
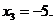3). При а = -1: аналогичная система, при х ≥ 0 графиком является парабола ветви вниз.

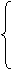
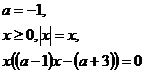из последнего уравнения

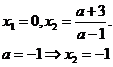в силу симметричности

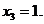Ответ: а=2 ; х={-5;0;5},
       а=-1; х={-1;0;1}.

Для самостоятельной работы:
Задание 3.4. Найти все значения параметра а принадлежит R , при каждом из которых уравнение имеет ровно три различных действительных корня.
б) .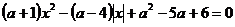
в) .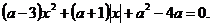

Задание 3.5. а) Найти все значения параметра а ∈ R , для каждого из которых уравнение 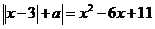имеет один действительный корень.

Решение: Данн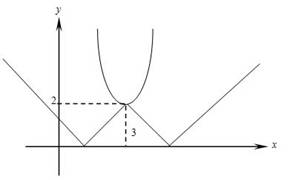ое уравнение удобно решить графически так как левая часть уравнения представляет из себя график функции 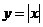со смещением вершины ( 0; 0 ) в точку ( 3; а ) Правая часть уравнения не зависит от параметра и ее графиком будет парабола ветви вверх. Для удобства построения 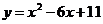выделим полный квадрат 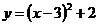. Вершина параболы имеет координаты ( 3; 2 ). Изобразим графическую модель данного уравнения , очевидно что первого координатного угла достаточно. Согласно правилам построения графиков содержащих модуль и условия задачи (единственный корень) получаем :

Очевидно, что уравнение имеет единственный корень в том случае, если: 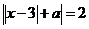, анализируя изображение при 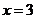получаем : 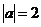, корень уравнения принадлежит первой четверти, тогда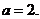

Для самостоятельного решения:
Задание 3.5. б) 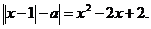в)

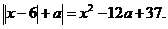
Задание 3.6. Найти все значения параметра а ∈ R , для каждого из которых сумма действительных корней заданного уравнения принимает наименьшее значение.
а )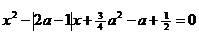

Решение: Данная задача относится к типу задач с ограничениями на корни квадратного трехчлена и сводится к системе рациональных неравенств. Для того , чтобы решить данное уравнение необходимо рассмотреть задачу о расположении корней квадратного трехчлена. Знак модуля содержит коэффициент при переменной х , значит графиком функции у =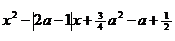 является парабола , ветви вверх. Сумма корней будет наименьшей , если оба корня отрицательны. Тогда для решения данной задачи (оба корня отрицательны) имеют место следующие утверждения.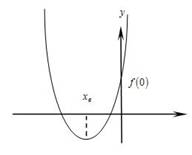

1. Уравнение имеет корни, если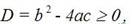
2. < 0,
3. f(0) > 0 .

Найдем значение дискриминанта : D = = .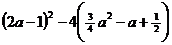

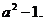Запишем систему неравенств отвечающих условию задачи :

Ответ : сумма корней уравнения наименьшая если a ∈ (-∞ ;-1].

Для самостоятельного решения:
Задание 3.6. б ) 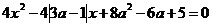в)