Пятое занятие!

Назад

ЦЕЛЬ: Отработать задачи на определение знаков корней квадратного трехчлена с использованием теоремы Виета для приведенных и не приведенных квадратных уравнений.

Задание 4.1. При каких значениях параметра p оба корня уравнения 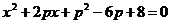отрицательны и различны?
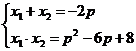Решение: I способ: Если корни квадратного уравнения существуют то D ≥ 0. Вычислим значение дискриминанта: D=. По теореме Виета . Так как оба корня отрицательные их сумма будет принимать отрицательное значение, а произведение положительное значение и с учетом D ≥ 0 систему неравенств:
⇔ ⇔
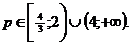
II способ: Решим используя правила расположения корней квадратного трехчлена. Если оба корня отрицательны, то графически данное уравнение имеет вид:

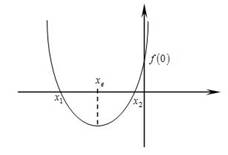
Проанализировав условия, запишем систему неравенств ⇔ ⇔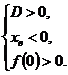
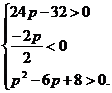Ответ: при уравнение имеет два отрицательных различных корня.

Задание 4.2. При каких значениях параметра a, корни уравнения 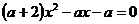симметричны относительно х=1?
Решение: Если 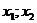- корни уравнения то по теореме Виета 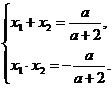. Если корни симметричны относительно х=1, то 1 – середина отрезка 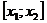запишем систему с тремя неизвестными: . Из I и III ⇔ .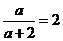
Подставив в I и II получаем: ⇔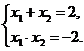
Решим второе уравнение: D = 12, тогда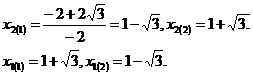
II способ (более простой). Зная, что график квадратичной функции имеет ось симметрии 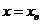, условие задачи равносильно системе
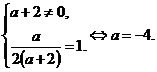
Корни уравнения вычислим, применив теорему Виета.
Ответ: при а= -4 корни 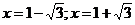симметричные относительно х=1.

Задание 4.3. При каких значениях параметра a, сумма корней уравнения 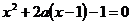равна сумме квадратов его корней?
Решение: 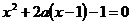⇔ 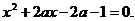. Если корни существуют, тогда по теореме
Виета по условию получаем систему с тремя неизвестными
⇔ ⇔ .
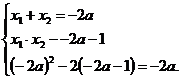Решаем последнее уравнение: 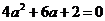D = 4; .
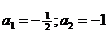Возвращаясь к системе рассмотрим два случая:

1)          2)  

Задание 4.4. каких значениях параметра a, разность корней уравнения 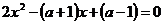равна их произведению?
Решение: Если квадратное уравнение имеет корни, то исходя из вопроса задачи и используя теорему Виета составим систему уравнений:
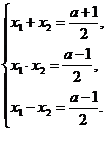⇔ I+III получаем ⇔ ⇔ ⇔
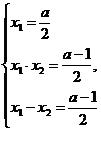Из второго уравнения системы а=2 подставляя в первое получаем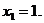
Ответ: при а = 2 разность корней уравнения равна их произведению.

Задание 4.5. При каких значениях параметра a уравнение 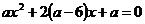имеет два положительных различных корня?

Решение:

I способ. Если уравнение имеет два различных корня, то а ≠ 0 и D>0. Вычислим значение дискриминанта: 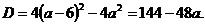Так как корни положительные теорема Виета имеет вид:    Запишем систему, состоящую из трех неравенств:   ⇔  ⇔.

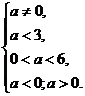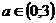
Ответ: при а ∈ (0;3) уравнение имеет два различных положительных корня.

II способ. (используя свойства расположения корней)
Так как параметр является коэффициентом при 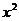, ветви графика квадратичной функции могут быть направлены как вверх, так и вниз. По условию оба корня положительны, графически положение корней можно изобразить следующим образом: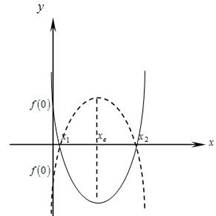

1 случай (ветви вверх) равносилен системе: ⇒  ⇒  ⇒ .

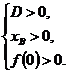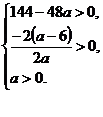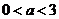
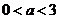2 случай (ветви вниз) равносилен системе: ⇒  ⇒ ⇒

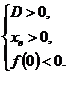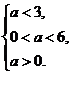Ответ: при а ∈ (0; 3) уравнение имеет два различных положительных корня.

Задание 4.6. Найти все значения параметра k, при которых корни уравнения 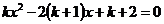имеют различные знаки?

Решение: Если уравнение имеет два корня , то D>0 и k ≠ 0. Вычислим значение дискриминанта 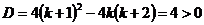 при любых значениях k, то есть уравнение всегда имеет два корня. По условию корни различных знаков, следовательно их
произведение отрицательно. По теореме Виета 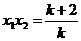 тогда имеет место неравенство:  ⇒

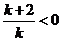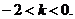
Ответ: при k ∈ (-2;0) уравнение имеет два корня разных знаков.

Задание 4.7.а) Найти все значения параметра а, при которых уравнение 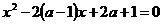имеет корни, определить знаки корней в зависимости от параметра.

Решение: Данное уравнение приведенное, квадратное и имеет корни, если D ≥ 0. Найдем значение дискриминанта . D ≥ 0 ⇔ 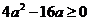. Решая методом интервалов, получаем 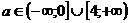. Рассмотрим следующие возможные случаи в зависимости от параметра:

 1. D = 0.     а=0:           или           2. а=4: 

Единственный, отрицательный корень.              Единственный, положительный корень. 

2. D>0 существует два различных корня, для определения знаков воспользуемся теоремой Виета

- если оба корня положительны, то сумма и произведение корней положительны, составляем систему:

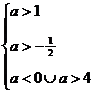 ⇒  ⇒ ⇒ а > 4.

- если оба корня отрицательны, сумма корней отрицательна, произведение положительно, составляем систему:

 ⇒  ⇒  ⇒

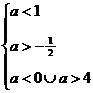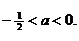
- если корни разных знаков, то это равносильно условию: произведение корней отрицательно. Составляем систему:

 ⇒  ⇒  ⇒

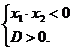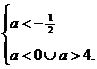если один из корней равен нулю, это равносильно, что произведение равно нулю.  По теореме Виета  ⇒ ⇒  ⇒ 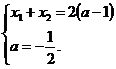так как один из корней равен нулю, следовательно, второй корень равен  (-3). Значение 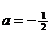 удовлетворяет условию D>0.

Ответ: 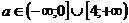уравнение имеет корни
а=0 один отрицательный корень
а=4 один положительный корень
         а=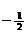 один корень отрицательный, второй равен нулю
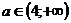  два положительных корня
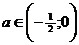  два отрицательных корня
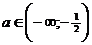 два корня разных знаков.
Задание 4.7. б) При каких значениях параметра а, уравнение 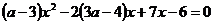имеет корни, определить знаки корней в зависимости от параметра.

Решение: Данное уравнение отличается от предыдущего тем, что параметр присутствует при переменной 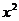, то есть при определенном значении параметра уравнение может быть линейным, его тоже нужно проверить на наличие корней.

Если квадратное уравнение имеет корни, то D ≥ 0; a≠3/ Вычислим з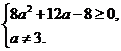начение дискриминанта 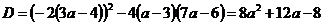. D ≥ 0; а≠3 ⇔ ⇔ 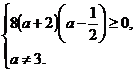решаем методом интервалов:

Два корня существует, если

Рассмотрим следующие возможные случаи, в зависимости от параметра:

1.  D = 0, а =-2: 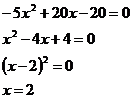один положительный корень

D = 0, а= 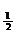: один положительный корень

2. Если а = 3 :  х = 1,5  Один положительный корень.

3. Если D>0, то существует два корня, для определения знаков воспользуемся теоремой Виета:

- оба корня положительные, что равносильно системе:

⇔

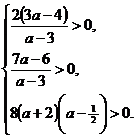
- оба корня отрицательные, что равносильно системе:

⇔

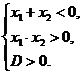Совместных решений нет.

- оба корня разных знаков, что равносильно системе:

⇔

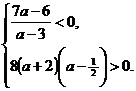
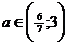
4. Один из корней равен нулю, что равносильно – произведение равно нулю.

 данное значение удовлетворяет условию существования корней D ≥ 0. Подставим данное значение параметра в равенство , выражающее сумму корней: 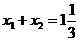. С учетом того, что один из корней равен нулю, второй корень равен  .

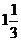Ответ: уравнение имеет корни, если
а=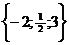   один положительный корень
два положительных корня<
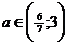корни разных знаков
   один из корней положительный, второй равен нулю.

Задание 4.7. Для самостоятельной работы.

в) Найти все значения параметра а, при которых уравнение 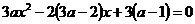 имеет корни. Определить знаки корней в зависимости от значений параметра.

Задание 4.8.* При каких значениях параметра а, сумма кубов корней уравнения 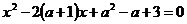будет наименьшей?

Решение: Уравнение имеет корни, если D ≥ 0. Вычислим значение дискриминанта 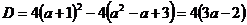. Так как D ≥ 0 ⇔  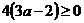⇔ 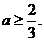Пусть  и 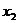корни уравнения, тогда по теореме Виета .Зададим функцию, выражающую сумму кубов через параметр а.
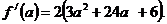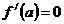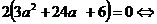
Исследуем данную функцию на наибольшее, наименьшее значение через производную   Найдем критические точки производной .  Решая последнее равенство через формулы корней квадратного уравнения находим 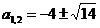. Оценим знаки производной:

По рисунку видно, что критические точки не попадают в условие D ≥ 0, следовательно функция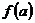 на полуинтервале  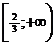сохраняет знак и является возрастающей, значит наименьшее значение  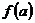достигается при .

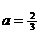Задание 4.9.* При каких значениях параметра а, сумма кубов корней квадратного уравнения будет наибольшей и наименьшей?

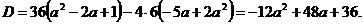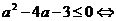
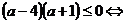
Решение: Уравнение имеет корни, если D ≥ 0. Вычислим значение дискриминанта  D ≥ 0 ⇔ 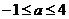. Если 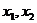корни уравнения, то потеореме Виета  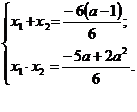Выразим сумму кубов через а, зададим функцию: Исследуем данную функцию на возрастание, убывание. 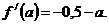 Критические точки производной а=-0,5. Определим знаки производной на интервалах:

Критическая точка принадлежит интервалу 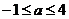и при переходе через , меняет свой знак.
Найдем значение производной в критической точке и на концах отрезка: - наибольшее значение; 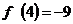- наименьшее значение.

Ответ: при а= 4 сумма кубов корней будет наименьшей;
             при а = - 1 сумма кубов корней будет наибольшей.

Задание 4.10.* Доказать, что если a, b, c – длины сторон треугольника, то уравнение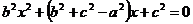 не имеет корней.

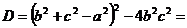
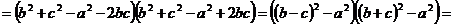
Решение: Квадратное уравнение не имеет корней, если дискриминант принимает отрицательное значение. Вычислим дискриминант 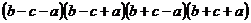. Так как  а, b ,с – длины сторон треугольника, то, следовательно D < 0 при любых значениях параметра, таким образом уравнение корней не имеет, что и требовалось доказать.

Задание 4.11.* При каких значениях параметра а, уравнение 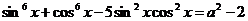имеет корни?

Решение: Данное уравнение рационально решать графически, так как правая и левая части разные по качеству функции. Для построения графиков упростим левую часть уравнения:

Первоначальное уравнение равносильно 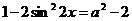⇔ Построим графики функций  Для удобства построения первого графика понизим степень тригонометрической функции: Графиком данной функции является волна косинусоиды, с периодом , отображенная симметрично относительно сои 0х, со смещением вверх на 1 вдоль оси 0у. Графиком функции 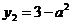- является прямая, параллельная оси 0х. Построим графики функций в одной системе координат:

Пунктирной линией показано расположение прямой 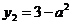, очевидно, что уравнение имеет корни, если  ⇔

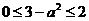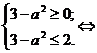
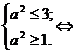
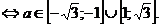
Ответ: уравнение имеет корни, если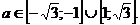

Задание 4.12.* При каких значениях параметра а, корень уравнения 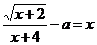единственный? Найти корень.

Решение: Уравнение 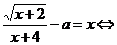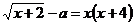; при х ≠ - 4.

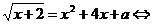
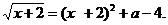
Построим графическое решение данного уравнения. Рассмотрим функцию 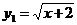- графиком является лежачая полу парабола, вершина (-2; 0). Функция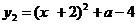- графиком является парабола, ветви вверх, вершина (-2; а-4). Строим:

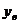По графику видно, что единственный корень есть в двух случаях I и III. Для первого (I) Для случая (III)  точки касания нельзя определить однозначно, поэтому решим данное уравнение аналитически.

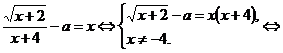
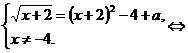
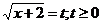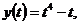    пусть , а 4-а=b, тогда уравнение в последней записи системы примет вид:  Рассмотрим функцию  исследуем ее на наибольшее и наименьшее значение, найдем экстремумы:  
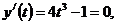
определим знаки производной и поведение функции:  

Функция 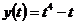 имеет один экстремум это точка min. Поэтому, чтобы уравнение  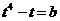имело единственное решение,  должно выполнятся условие: 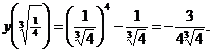  Получаем: 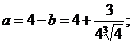так как ⇔ 

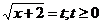Ответ: 1) уравнение имеет один корень, если 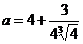 и а<4;
              2) при ;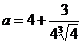    

Назад