Зачетная работа по теме: "Квадратные уравнения с параметром".

Назад

Уровень А.

1. На рисунке изображен график квадратичной функции 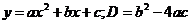то справедливы соотношения:

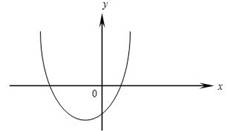
1) a > 0, D > 0, b < 0
2) a > 0, b > 0, c < 0
3) a > 0, D > 0, c > 0
4) D > 0, c > 0, b > 0
5) a > 0, b < 0, c > 0.

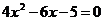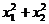2. Не вычисляя корней уравнения найти и .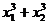

3. При каких значениях параметра m, корни уравнения 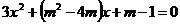равны по модулю, но противоположны по знаку.

4. Найти все значения параметра m, при которых оба корня уравнения 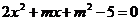меньше 1.

Уровень В.

1. Найти наименьшее целое значение параметра а, при котором система уравнений
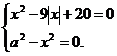не имеет решений.

2. Найти все значения параметра а, при которых корни уравнения 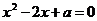удовлетворяют условию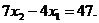

3. Найти все значения параметра а, при которых уравнение имеет единственный корень.

4. Найти все значения параметра k, при которых уравнение 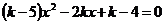имеет два корня, причем один из них меньше 1, а другой больше 2.

Уровень C.

1. Пусть 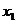и 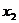- корни квадратного уравнения 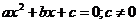. Выразить через коэффициенты a, b, c: 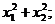; ; 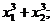; ; 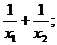; ; 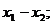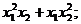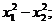ю

2. При каких значениях параметра a, уравнение 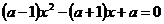имеет единственное решение, удовлетворяющее условию .

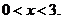3. Найти все значения параметра а, при каждом из которых уравнение 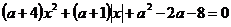имеет ровно три различных действительных корня.

4. Найти все значения параметра а, при которых вершины парабол 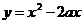и 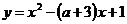лежат по разные стороны от прямой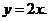

Ответы и краткие пояснения к решению зачетной работы.

Уровень А.

1) (1)

2)

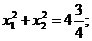
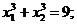
3) m = 0; (если свободный коэффициент равен нулю, то один из корней квадратного уравнения равен нулю, а по условию корни равны по модулю, но противоположны по знаку, либо оговорить условие, что свободный коэффициент не равен нулю, либо после нахождения значения параметра выполнить проверку).

4) .
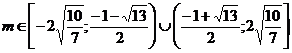Выполнение условия данной задачи равносильно системе: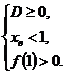

Уровень В.

1) 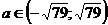; (приравнять левые части уравнений, квадратное уравнение не имеет корней, если его дискриминант отрицательный. Решая неравенство, найти значение параметра).

2) а =- 15; (составить систему, состоящую из трех уравнений с тремя неизвестными, применив теорему Виета).

3) а = 5; (решить графически).

4) k ∈ (5; 24);(составить систему, удовлетворяющую расположению корней, согласно условию. Не забыть, что в данной задаче, ветви параболы могут быть направлены как вверх, так и вниз).

Уровень C.

1) Для нахождения разности корней, вычислить значения 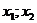через дискриминант.

2) 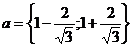; (составить две системы неравенств, используя задачи о расположении корней).

3) ; 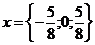(условие существования трех корней для квадратичной функции, содержащей знак модуля). ;

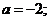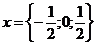
4) 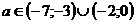. (Сложность решения данной задачи состоит в том, что расположение вершины параболы 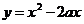на участках ;
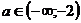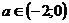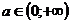и - различное, поэтому для решения, рассматриваются все три случая, составляются три системы неравенств).

Назад